Description

https://oj.leetcode.com/problems/linked-list-cycle/

https://oj.leetcode.com/problems/linked-list-cycle-ii/

Solution

Solutions to both problems are based on slow-fast pointers. If there is a cycle, the the slow and fast pointer will meet finally.

class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode * slowPt = head, * fastPt = head;
        while(fastPt){
            slowPt = slowPt->next;
            fastPt = (fastPt->next)?fastPt->next->next:NULL;
            if (slowPt == fastPt)
                break;
        }
        if (fastPt == NULL)
            return false;
        return true;
    }
};

For the second problem, we have to find where the circle starts, so let us look at the figure below and do some math work.

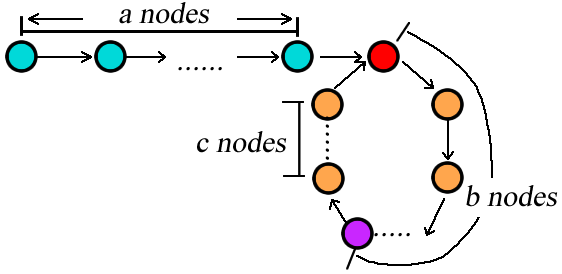
Supposed that the slow and fast pointers met at the purple node, as the fast pointer is twice faster than slow pointer, we have the relationship

Then we have

If we have a new pointer starting from the head and the other pointer starting at the node where slow and fast pointers meet (i.e., the purple node), they will meet at red node, because $a\%(b+c) = c$ and purple node is $c$ nodes far from the red node.

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {

		ListNode *p1 = head, *p2 = head;
		while(p2){
			p1 = p1->next;
			p2 = (p2->next)?p2->next->next:NULL;
			if (p1 == p2)
				break;
 		}
 		if (p2 == NULL)// no cycle
 		    return NULL;
		p2 = head;
		while(p1 != p2){
			p2 = p2->next;
			p1 = p1->next;
 		}
		return p1;
    }
};