Description
https://oj.leetcode.com/problems/largest-rectangle-in-histogram/
Analysis & Solution
This is a pretty interesting question. The best solution using stack looks very tricky at the first look. This post will give some analysis of what is the thought under that solution and a more straightfoward solution using exactly the same thought, the time complexity of which is also . This may help you know how to come up with that kind of solution for other problems.
Solution 1
The simplest method I can come up is that we enumerate each pair of start point and end point and compute the area of the rectangle between and . The area only depends on and the minimum bar height.
maxArea = 0
for i = 0..n-1
for j = i..n-1
curArea = min(height, i..j) * ( j - i + 1) /* O(n) operation */
maxArea = max(curArea, maxArea);Thus this is a naive solution.
Key Observation: Given several consecutive bars, the bar with the mimimum height decides the area of the rectangle formed by those bars.
Solution 2
It is very easy to notice that there is lots of redundant computation involved in solution 1. When we compute the minimum height between bar and , we do not need to iterate from to every time, if we record, e.g. the min height between and in some variable . Then
This is a solution.
Solution 3
Let us look at this problem in a slightly different way. Still following the thought the minimum bar is the key bar that decides the area of a rectangle, what is the maximum rectangle that has bar as the minimum bar?
The example below gives the answer
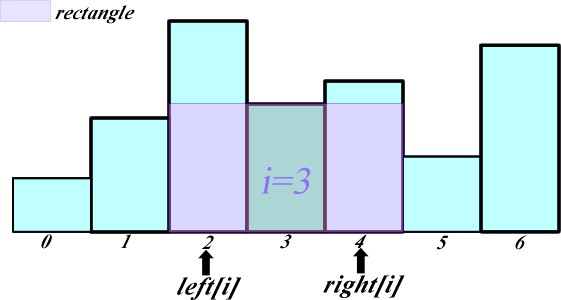
In this figure, all the bars on the left side (including) the bar cannot be in the rectangle, because the bar is the first bar on the left side of bar . Similarly, all the bars on the right side (including) the bar cannot be in the rectangle.
This is exactly how we locate the left and right boundaries of the rectangle taking bar as the shortest one.
Then it is trivial to compute the area of the rectangle taking bar as the shortest one
and
maxArea = 0
for i = 0..n-1
for right = i..n-1 // find right boundary
if height[i] > height[right]
break
for left = i..0 // find left boundary
if height[i] > height[left]
break
right --; left ++;
maxArea = max(maxArea, (right - left + 1) * height[i]));The key idea here is that in each outer loop, we take each bar as the shortest bar in the rectangle and find the left boundary and right boundary of the maximum rectangle that takes this bar as the shortest bar. Then we compute the area and update .
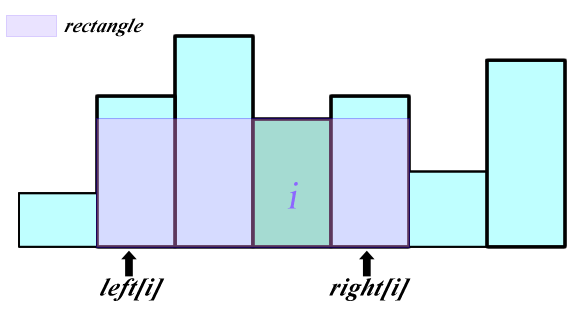
NOTE: The following two more efficient algorithms are also doing the same thing (locate left and right boundaries), but in a smarter way.
Solution 4
We start from an example to show how to speed up solution 3
bar height: 0, 1, 2, 3, 4, e.g. height[i] = i
In solution 3, when we compute the right boundary of , we have to iterate from 2 to 4. However an easy observation is that as , .
In summary,
- , if
- height[i] <= height[i+1]$$
However until now we only know , if . What exactly is ?
The whole procedure of computing goes here
- Step1 initialize j = i + 1
- Step2 check if or ,
- 2.1 if so, END
- 2.2 if not,
- 2.2.1 j = right[j] + 1
- 2.2.2 go back to Step2
- Step3 right[i] = j - 1
We use an example to illustrate how the algorithm goes
bar height: 0, 1, 2, 3, 4, 2, 3
right: 6, 6, 5, 4, 4, 6, 6
Suppose that we are trying to compute ,
- Step1: we find that , then we go to .
- Step2: We find that , then we go to .
- Step3: As then we go to .
- Step4, , so
It is the same procedure to find the left boundary and here is the code.
1 class Solution {
2 public:
3 int largestRectangleArea(vector<int> &height) {
4 int maxArea = 0;
5 int n = height.size();
6
7 int left[n]; // array of left boundary for each bar
8 int right[n]; // array of right boundary for each bar
9
10 //looking for the left boundary
11 for (int i = 0; i < height.size(); ++ i){
12 left[i] = i;
13 int j = i-1;
14 while(j >= 0 && height[j] >= height[i]){
15 left[i] = left[j];
16 j = left[j]-1;
17 }
18 }
19 //looking for the right boundary
20 for (int i = n-1; i >= 0 ; -- i){
21 right[i] = i;
22 int j = i+1;
23
24 while(j < n && height[j] >= height[i]){
25 right[i] = right[j];
26 j = right[j]+1;
27 }
28 maxArea = max(maxArea, (right[i] - left[i] + 1) * height[i]);
29 }
30
31 return maxArea;
32
33 }
34 };Time complextiy
It is a little bit complicated (but not hard) to prove the time complexity is . I may try to write a formal proof later. Here is a simple example of how redundant computation is avoided and may give you some intuition.
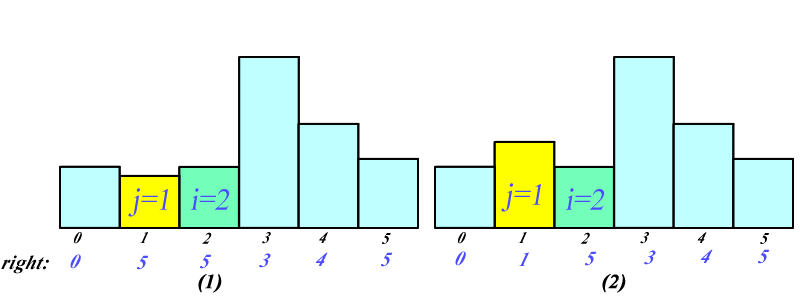
In this example, it is pretty painful to compute , because we have to first go to 3, then 4, then 5, which is a procedure. However, when it comes to the computation of after is computed, life is much easier
- in (1), , then only 1 operation is enough
- we go to , but find , DONE.
- in (2),
- , DONE
Actually, after we go through 3, 4, 5 during the computation of we will never have to go through 3, 4, 5 any more in our later computation of . As the total number of bars we can go through is , the algorithm is an algorithm.
More thoughts
The thought of solving this probelm is also kind of similar to Trapping Rain Water. In TRW, we consider about each bar and try to compute the number of units of the water this bar holds by locating the highest bar on both left side and right side respectively, while in this problem, for each bar, we are trying to locate left and right boundaries.
Solution 5
Solution 5 still sticks on the key idea that we consider each bar as the minimum bar in a rectangle and try to compute the corresponding area by locating its left boundary and right boundary. It is easier to see the time complexity is for this solution.
Solution 4 and 5 look very different from each other, but they are not.
In solution 4, we enumerate each bar as the minimum bar in a rectangle, compute the area, and then update the .
In solution 5, we enumerate each bar, and check if this bar can be a right boundary for any bar on the left side of it. If so, we go back to the stack to check which bars use this bar as right boundary. One brilliant thing about this solution is that we implictly save the information about their left boundaries of those bars in the stack. Then we can compute the area of maximum rectangle for each bar and find the maximum area.
Please refer to my following implementations to figure out the details of this algorithm.
1 class Solution {
2 public:
3 int largestRectangleArea(vector<int> &height) {
4 stack<int>stk;
5 int maxArea = 0;
6 height.push_back(0);
7 int n = height.size();
8 for (int i = 0; i < n; ++ i){
9 while (!stk.empty() && height[stk.top()] > height[i] ){
10 // the index of minimum bar in the rectangle that we currently consider
11 int curIdx = stk.top();
12 stk.pop();
13 int leftBoundary = (stk.empty())? 0 : stk.top()+1;
14 // the right boundary is obviously i-1
15 int curArea = (i - leftBoundary) * height[curIdx];
16 maxArea = max(maxArea, curArea);
17 }
18 stk.push(i);
19 }
20
21 return maxArea;
22 }
23 };Solution 6
Solution 6 is an divide-and-conquer algorithm, which can be found at http://www.geeksforgeeks.org/largest-rectangle-under-histogram/.

